Branch Current Analysis Method

by

The branch current analysis method is a circuit analysis technique that involves combined application of Kirchhoff’s Current and Kirchhoff’s Voltage law with Ohm’s law and the combined application of Ohm’s Law. The first step in applying Branch Current analysis is assuming the directions of currents. Next steps involve writing of equations and describing their relationships to each other through Kirchhoff’s current law (KCL), Kirchhoff’s voltage law (KVL), and Ohm’s law. The final steps involve solving all equations to find branch currents. Electrical Engineering Online article on Branch Current Analysis Methods lets you master the technique to analyze circuits using Branch Current analysis.

Let’s directly dive into this step-by-step example:

Branch Current Analysis Example Circuit

Problem Statement: Find the current in each branch of the circuit.

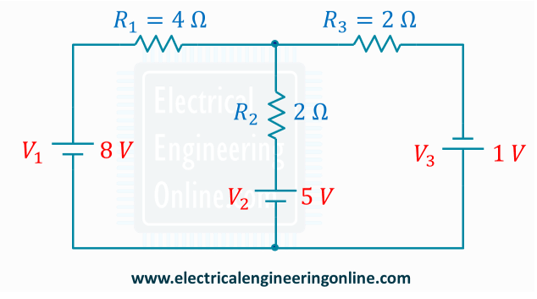
Solution

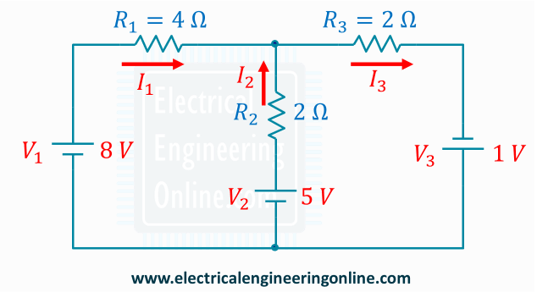
Step 1: Assign the current I1, I2, and I3 to branches as below:

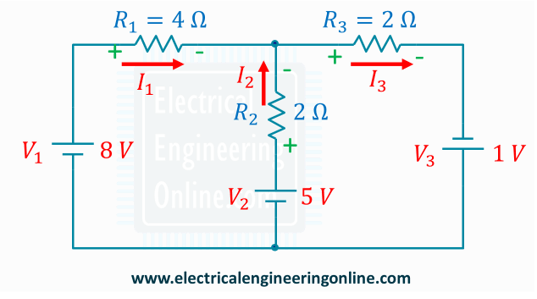
Step 2: Indicate the polarity of voltage drops using the assumed currents current I1, I2, and I3 in Step 1.In the figure below the polarities are indicated using green colored (+ and -) signs.

Step 3: Application of KVL to the left loop

8 V – 4I1+2I2  – 5V=0

Solving and rearranging the above we obtain equation (1):

4I1-2I2 = 3 … (Equation 1)

Step 4: Application of KVL to right loop

5 V- 2I2-2I3+1 V=0

Solving and rearranging the above we obtain equation (2):

2I2+2I3=6 … (Equation 2)

Step 5: Application of KCL to the central node

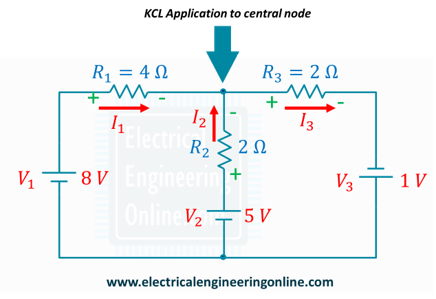
The application of KCL to the central node yields Equation 3

I1+I2=I3 … Equation 3

Step 6: Solving Equations

Let’s reuse I3 from Equation 3 in Equation 2

2I2+2I3=6 … (Equation 2)

2I2+2(I1 + I2)=6

2I1 + 4I2 = 6 … (Equation 4)

Let’s add Equation 1 and subtract 2*Equation 4 from it

4I1-2I2 – 2(2I1 + 4I2) = 3 – 2(6)

4I1-2I2 – 4I1 – 8I2 = 3 – 12

-10I2 = -9

or I2 = 9/10 = 0.9 A

Let’s find I1 by using I2 = 0.9 A back in equation 1

4I1-2I2 = 3;

4I1-2(0.9) = 3; 4I1-1.8 = 3

4I1 = 4.8; I1 = 1.2 A

Let’s use I2 = 0.9 A & I1 = 1.2 in Equation 3

I1+I2 = I3

1.2 + 0.9 = I3

I3 = 2.1 A

So that was all about the circuit analysis using Branch Current Analysis Method.

Leave a Comment